nanDECK - Tutorial C

This tutorial was written for nanDECK 1.8a (or later versions). First, we define a label:

[LAB1]="Alpha"

This label can be used later with script commands like:

FONT="Arial", 72, "", "#000000"
TEXT="1", [LAB1], 0, 0, 6, 9, "center", "center", 90

For this result:

Easy, no? But we can add some parameters to the label's definition, like a repeat number:

[LAB1]3="Alpha"
FONT="Arial", 32, "", "#000000"
TEXT="1", [LAB1], 0, 0, 6, 9, "center", "center", 90

And the label now is evaluated as "AlphaAlphaAlpha". The next step is introducing another parameter, a label prefix for permutations and combination, but before we must define more than one object ("Alpha") using "|" character:

[LAB1]="A|B|C"

Now if we want a combination of two objects from our set of three, we can write:

C[LAB1]2="A|B|C"

This label will be translated into "AB|AC|BC" in the code execution (every combination of two elements from a set of three). If we want a permutation instead, we can write:

P[LAB1]2="A|B|C"

And the resulting label will be "AB|AC|BA|BC|CA|CB". Remember, in a permutation the order of the elements is important, AB is different from BA.

How we can use this label? With a code like this we can have all permutation of three elements, one on every card:

P[LAB1]3="A|B|C"
FONT="Arial", 72, "", "#000000"
TEXT="1-6", [LAB1], 0, 0, 6, 9, "center", "center", 90

By pressing "Validate deck" button, the program gives you this intermediate code:

P[LAB1]3="A|B|C"
FONT="Arial", 72, "", "#000000"
TEXT="1-6", "ABC|ACB|BAC|BCA|CAB|CBA", 0, 0, 6, 9, "center", "center", 90

And these are the cards (resulting from "Build deck" function):

But you can have repetitions as well, with CR and PR prefix. This code:

CR[LAB1]3="A|B|C"

gives you this label: "AAA|AAB|AAC|ABB|ABC|ACC|BBB|BBC|BCC|CCC". And this code:

PR[LAB1]3="A|B|C"

will translate in:

"AAA|AAB|AAC|ABA|ABB|ABC|ACA|ACB|ACC|BAA|BAB|BAC|BBA|BBB|BBC|BCA|BCB|BCC|CAA|CAB|CAC|CBA|CBB|CBC|CCA|CCB|CCC

Remember that you aren't limited to single letter elements. You can write:

PR[LAB1]3="Alpha|Beta|Gamma"

and you obtain this monstruosity (I've inserted some newline):

"AlphaAlphaAlpha|
AlphaAlphaBeta|
AlphaAlphaGamma|
AlphaBetaAlpha|
AlphaBetaBeta|
AlphaBetaGamma|
AlphaGammaAlpha|
AlphaGammaBeta|
AlphaGammaGamma|
BetaAlphaAlpha|
BetaAlphaBeta|
BetaAlphaGamma|
BetaBetaAlpha|
BetaBetaBeta|
BetaBetaGamma|
BetaGammaAlpha|
BetaGammaBeta|
BetaGammaGamma|
GammaAlphaAlpha|
GammaAlphaBeta|
GammaAlphaGamma|
GammaBetaAlpha|
GammaBetaBeta|
GammaBetaGamma|
GammaGammaAlpha|
GammaGammaBeta|
GammaGammaGamma"

UPDATE!

With version 1.9b, I've introduced a couple of interesting features that can be used with the combination's engine: first, you haven't to specify beforehand the size of the deck. If you don't know how many cards will result from this:

PR[LAB1]3="A|B|C"

In the range parameter of a directive you can use this syntax:

TEXT=1-{(LAB1)},[LAB1],0,0,6,9,0

Remember, { and } are the expression's delimiters, ( and ) are the label's delimiters. The expression 1-{(LAB1)} will be converted in 1-27 at run-time.

Second, you can extract substrings from a label, using this syntax:

[LABEL:start character,number of characters]

How this can be used? If you want to create all combinations of plains, woods and mountains in a square tile with 4 triangles, you can use a script like this:

cardsize=4,4
[quarter1]=0,0,2,2,0,4
[quarter2]=0,0,4,0,2,2
[quarter3]=4,0,4,4,2,2
[quarter4]=0,4,2,2,4,4

pr[schema]4=P|F|M
[all]=1-{(schema)}

[color_p]=#00FF00
[color_f]=#008000
[color_m]=#C0C0C0

triangle=[all],[quarter1],[color_[schema:1,1]]
triangle=[all],[quarter2],[color_[schema:2,1]]
triangle=[all],[quarter3],[color_[schema:3,1]]
triangle=[all],[quarter4],[color_[schema:4,1]]

With [color_schema:1,1]] the program extracts the first letter of the label, adds color_ before it, and it will result in a color label.

This is the result (four pages):

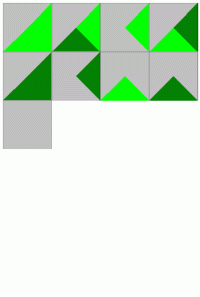
You can download this script from here and the PDF from here.

UPDATE!

The last script creates 81 tiles, but they aren't unique: you'll find a lot ot rotated tiles. With version 1.9c I've introduced a flag useful to remove rotations from combination/permutation output (only if applied in circular pattern); if you change this line:

pr[schema]4=P|F|M

with this line (adding an "x"):

prx[schema]4=P|F|M

The output will be made of 24 unique tiles.

Bye,
/\/and